Durch die Integration der Feldmasse in die Gravitationswirkung
entsteht ein korrigiertes Gravitationsgesetz, das in seinem Verlauf
für sehr große Distanzen von der Newtonschen Beschreibung
der Gravitation abweicht.
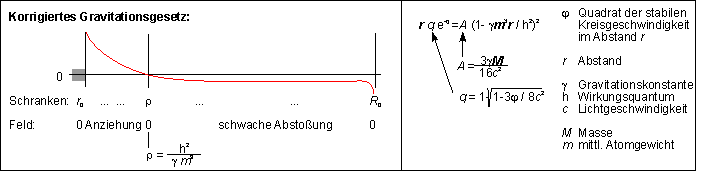
Ferner wird der Bereich seiner Gültigkeit durch eine obere
(R0) und eine untere (r0) Realitätsschranke
begrenzt.

Im Bereich zwischen der oberen Grenzdistanz R0 und ρ muß jede Masse eine sehr schwache Abstoßung überwinden, wenn sie sich der Feldquelle nähern will. Da diese Wirkung nur für sehr große Distanzen auftritt, ist sie praktisch nicht beobachtbar. Allerdings kann die Größe der astronomischen Rotverschiebung als Ergebnis dieser Abstoßung rechnerisch bestätigt werden (siehe unten).
Ab ρ entspricht der Feldverlauf in guter Näherung dem Verlauf der Newtonschen Approximation. Die von uns beobachtbaren empirischen Prozesse spielen sich in diesem Bereich ab.
Die korrigierte Form des Gravitationsgesetzes spielt eine Schlüsselrolle bei Heims mathematischen Berechnungen, denn für ihn ist die Gravitation das einzige physikalische Hintergrundphänomen, das alle physikalischen Wirkungen begleitet. (Dieser Umstand ergibt sich aus der Äquivalenz von Gravitation und Trägheit und der Äquivalenz von Masse und Energie. Demnach können alle Energiephänomene durch Materiefeldquanten ausgedrückt werden).

Wenn die Gravitation das allgemeine Hintergrundphänomen der Welt
ist, dann kann es keine Welt außerhalb der Grenzen der Gravitation
geben. Demzufolge leitet Heim das Kleinste in der Welt vom
Gravitationsgesetz ab – die geometrische Letzteinheit.
Zu diesem Zweck untersucht er, ob es eine letzte geometrische
Größe gibt, die auch beim Verschwinden aller Massen im leeren
Raum bestehen bleibt. Eine solche konstante Größe ergibt sich
beim Übergang der Masse gegen 0, wenn man das Produkt zwischen der
unteren Realtitätsschranke des Gravitationsgesetztes und der
Komptonwellenlänge dieser verschwindenden Masse bildet.
Interessanter Weise ist diese geometrische Letzteinheit eine
Fläche. Sie liegt ungefähr in der Größenordnung des
Quadrats der Planckschen Länge. (Heim verwendete für sie den
Buchstaben τ, weil dieser zufällig auf seiner Schreibmaschine
vorkam).
Der Zahlenwert dieses Metrons (6,15 * 10-70 m2) beschreibt die geometrische Letzteinheit des leeren Raumes, in dem keine Masse existiert. Der reale physikalische Raum ist demgegenüber immer gekrümmt, wodurch die Elementarflächen je nach Felddichte mehr oder weniger verdichtet („kondensiert“) werden.
Ebenso wie das Kleinste der Welt leitet Heim auch das
Größte unserer Welt aus den Grenzen des Gravitationsgesetzes
ab – nämlich den maximalen Durchmesser unserer physikalischen
Welt.
Wenn man die obere Grenze R0 des Gravitationsgesetzes
für die kleinste denkbare Masse (Elementarmasse) berechnet,
erhält man den größten Durchmesser, für den das
Gravitationsgesetz real existiert.

Nach Heim ist die Rotverschiebung das Ergebnis des korrigierten
Gravitationsgesetzes. Demnach muss jedes Teilchen dieser Welt in
erster Linie gegen die abstoßende Gravitationskomponente von fast
der ganzen restlichen Welt anfliegen. (Das entspricht dem Feldverlauf
zwischen ρ und R0.) Das verbraucht Energie, wodurch jedes
Photon bei dieser Reise langwelliger wird.
Heim setzt die geschätzte mittlere Massendichte des Universums in
die Formel ein und erhält als Ergebnis den Hubble Radius, also den
Radius der sichtbaren Welt. Jedes Photon, das von weiter her kommt, hat
hinter diesem Radius seine komplette Energie abgegeben.
Die beobachteten Ausnahmen in der Rotverschiebung sind mit diesem Modell
lediglich das Ergebnis von inhomogener Massendichte, und deshalb sehr
plausibel.
