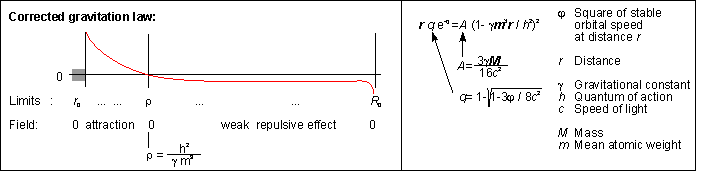
The integration of the field-mass into the gravitation leads to a corrected
law of gravitation, which deviates from Newton's description for very large
distances.
Furthermore, its range of validity now has an upper (R0)
and a lower limit (r0), called reality barriers.

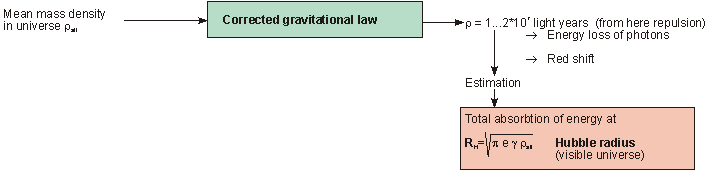
Any mass located in the region between the upper boundary distance R0 and ρ must overcome a very weak repulsion force if it wants to approach the field source. Since this effect occurs only at very large distances, it is practically unobservable. However, the value of the astronomical redshift can be recognised as a result of this repulsion by calculating it with Heim's corrected gravitational law (see below).
For distances smaller than ρ, the field is now a good approximation of Newton's approximation. All empirical processes in space that we can observe take place within this region.
This corrected law of gravitation plays a key role in Heim's mathematical calculations because, according to Heim, gravitation is the only physical background phenomenon that accompanies all physical effects. (This is a consequence of the equivalence of gravitation and inertia and a second equivalence of mass and energTherefore all energy phenomena can be expressed by matter-field-quanta).

Here is another fundamental idea of Burkhard Heim. He says:
If gravity is the general background phenomenon of the physical
world, then there can be no world outside the limits of
gravity!
Therefore with this law it is now possible to
determine both the smallest thing in the world (fundamental geometrical
unit) and the largest thing existing – the diameter of the whole
world.
Now we will see, how this is done.
Heim first investigated whether
there was a final geometric value that would remain even if all masses
disappeared into empty space. In fact, such a value is calculable during the
transition of mass towards 0, if one makes a product between the lower reality
limit of gravity and Kompton's wavelength of this infinitesimal mass.
Interestingly, this final geometric unit will then be a surface. It's size is
roughly the square of Planck's length. (Heim called it τ because this
letter happened to be on his typewriter).
The exact value of these metrons
(τ = 6.15 * 10-70
m2) describes the final geometrical unit of empty space,
where no mass exists. Real physical space – in contrast – is always curved, whereby these elementary surfaces
become more or less compressed (condensed
) depending on the density of all fields existing in this space.
Like the smallest thing in our world Heim also derives the largest
thing from the boundaries of the law of gravitation – the maximum
diameter of our physical world.
If you calculate an upper limit R0 of the
law of gravitation for the smallest mass conceivable mass (elementary
mass), you get the largest diameter for which the law of gravitation really exists.

Finally Heim found that the cosmic redshift is also a result of the corrected law of gravity. Therefore each particle of this world must approach primarily against the repulsive gravitational component of almost the entire rest of the world. (This corresponds to the field curve between ρ and R0.) This is using energy whereby each photon becomes longer in it's wavelength during this journey.
Heim inserted the estimated mean mass density of the universe into his
formula and than obtained as result the Hubble radius, which is the
radius of our visible world. Any photon coming from beyond this radius has lost all of
its energy.
Even the observed exceptions in red shift are now plausible with this model.
They are only a result of the inhomogenous mass density in space.