|
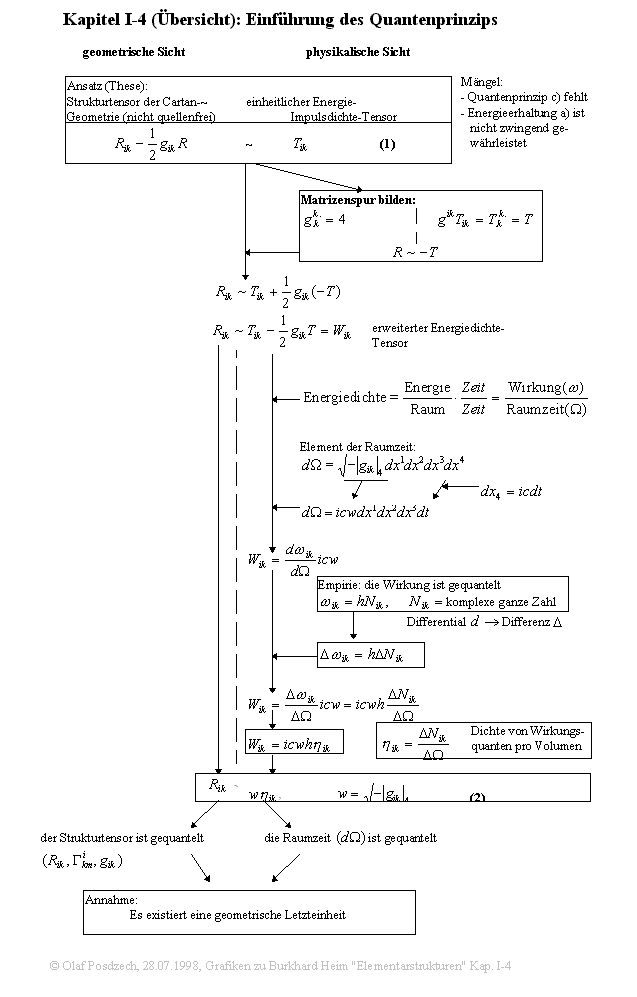
At this map you can pursue schematically the flow of thoughts described in chapter 1-4, where Heim states why a fundamental geometrical must exist.
Items of a general energy impulse density tensor describe all types of physical interactions (on the right), which can be understood on the other hand also geometrically as deformations of space (left side).
The type of this geometry is deduced in chapter 1-3. It results from the circumstance that every physical type of interaction produces its own metric.
The term power density
(Energiedichte) describes density
of energy per volume of space. The following is very simple now, and I
wonder why this still is not known in conventional physics: If you
extend this quotient both in counters and denominators with time, you
receive density of effect (energy * time) per space-time. Since we know
from experiences of quantum physics that effect is quantized also all
other values in this equation must be quantized, particularly all
coordinates of space-time.
Because on the left side a geometrical description is equivalent to this
physical description, this also must be transferred in a form of quantum
terms.
Installation of this quantum-physical description into the uniform structure tensor Heim shows in chapter II-1. From this the description of the material world in six physical dimensions results.