Die Heimsche Theorie ist eine radikal geometrische Beschreibung physikalischer Prozesse. Das heißt, sie versteht alle physikalischen Phänomene aus den inneren geometrischen Gesetzmäßigkeiten des sechsdimensionalen Raumes an sich.
Dieser Raum kann verschiedene gekrümmte Strukturen annehmen, die
ineinander übergehen können. (Diese Prozesse werden im Rahmen
der Heimschen Theorie mathematisch beschrieben). Unter bestimmten Randbedingungen
können solche Durchbiegungsprozesse zyklisch verlaufen. Der
Raum schwingt dann in einem bestimmten Bereich zwischen zwei verschiedenen
Partialstrukturen quasi immer hin und her. Dieses Volumen hat von außen
gesehen dann andere physikalische Eigenschaften als der leere Raum.
In Wirklichkeit sind diese Eigenschaften aber nicht das Ergebnis einer
Statik, sondern einer inneren Dynamik („Materie ist Kreisen auf der Stelle“).
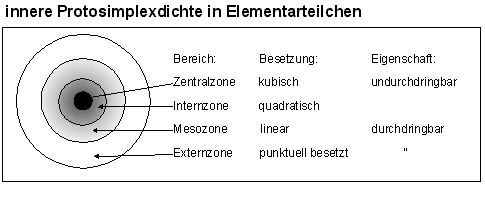
Die kleinste Einheit, die solche zyklischen Verdichtungen durchführen kann, ist ein Protosimplex. Protosimplexe treten jedoch nicht für sich isoliert auf, sondern können nur im Kontext anderer Protosimplexe existieren. Jedes Elementarteilchen ist ein solcher Verband von Protosimplexen. Ihre Dichte nimmt von innen nach außen ab.

Aus dieser Beschreibung wird klar, warum physikalische Versuche mit
„identischen“ Elementarteilchen zu periodisch schwankenden Ergebnissen
führen. Schließlich existiert demnach in jedem Teilchen ein
dynamisches Innenleben, dass von jedem Experiment zu einem zufälligen
Zeitpunkt „erwischt“ wird.
Ferner wird deutlich, dass es zwar eine Internstruktur von Elementarteilchen
gibt (Protosimplexe), sie ist aber nur im Kontext des gesamten Teilchens
existent.
Deshalb sind zum Beispiel keine isolierten Quarks beobachtbar, die
sich als Bruchstücke von Elementarteilchen erzeugen ließen.

Ein Elementarteilchen existiert demnach solange, wie der ständige Fluss zwischen allen seinen Partialstrukturen 1 und 2 aufrechterhalten bleibt. Wird der Fluss unterbrochen, beobachten wir von außen einen radioaktiven Zerfall.
Durch die mathematische Beschreibung dieser sechsdimensionalen Verdichtungsprozesse
gelangt Heim zu einer einheitlichen Massenformel und zur theoretischen
Begründung der Quantenzahlen aus diesen geometrischen Prozessen heraus.
Nach Heim sind alle bis heute beobachteten Elementarteilchen von der
Lösungsmenge seiner Massenformel bestätigt worden.